Kerala Plus One Maths Notes Chapter 1 Sets

I. Sets

Set is a well-defined collection of distinct objects.
Examples of sets.

• N: Set of Natural numbers.
• Z: Set of Integers.
• Q: Set of Rational numbers.
• R: Set of Real numbers.
• Z+: Set of Positive Integers numbers.
• Q+: Set of Positive Rational numbers.
• R+: Set of Positive Real numbers.

Representation of Sets:

1. Roster Form: All elements are listed, are separated by commas, and closed using brackets.
2. Set-builder Form: All elements of a set possess a single common property which is not possessed by any elements outside the set.
3. Venn Diagram: Here sets are represented by diagrams. These diagrams consist of rectangles and closed curves usually circles. The universal et is represented by a rectangle and its subsets by circles.

II. Types of Sets:

Empty set: Set contains no element, φ or {}.

Singleton set: Set containing one element.

Finite set: Set containing a definite number of elements.

Infinite set: Set containing an infinite number of elements..

Equivalent set: Sets containing an equal number of elements.

Equal set: Sets containing identical elements.

Subset: If every element of A is an element of B, denoted by A ⊂ B. For any set A, the set A and Empty set is a subset of A. If a set A has n elements, then it has 2n subsets.

Superset: B is a superset if A is a subset of B, denoted by B ⊃ A.

Proper Subset: If A ⊂ B and A ≠ B.

Power set: The set of all subsets of a set A, denoted by P(A). If n(A) = n, then n(P(A)) = 2n

Universal set: The superset of all subsets under discussion.

Intervals as subset of R:

1. [a, b] = {x : a ≤ x ≤ b}, closed interval.
2. (a, b] = {x : a < x ≤ b]
3. [a, b) = {x : a ≤ x < b}
4. (a, b) = {x : a < x < b}, open interval.

III. Operations on Sets

Union of Sets: The union of A and B is the set which consists of all elements of A and all elements of B except the common elements. In symbol we write as A ∪ B = {x : x ∈ A or x ∈ B}.
Venn diagram representation: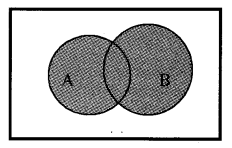

Properties:

1. A ∪ B = B ∪ A, Commutative.
2. (A ∪ B) ∪ C = A ∪ (B ∪ C), Associative
3. A ∪ φ = A, φ is the identity.
4. A ∪ A = A
5. U ∪ A = U

Intersection of Sets: The intersection of A and B is the set of common elements of both A and B.
In symbol, we write as A ∩ B = {x : x ∈ A and x ∈B}.
Venn diagram representation: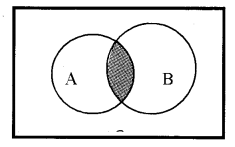

Properties:

1. A ∩ B = B ∩ A, Commutative.
2. (A ∩ B) ∩ C = A ∩ (B ∩ C), Associative
3. A ∩φ = φ
4. A ∩ A = A
5. U ∩ A = A
6. A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
7. n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
8. If A and B are disjoint, then n(A ∪ B) = n(A) + n(B)
9. n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(C ∩ A) + n(A ∩ B ∩ C)

Difference of Sets: The difference of the sets A and B in this order is the set of elements which belongs to A but not to B, denoted by A – B = {x : x ∈ A and x ∉ B}
Venn diagram representation: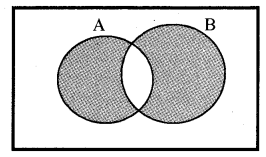

Property: A – B ≠ B – A

Complement of a Set: The complement of a set A is the set of all elements of U which are not in A, denoted by
A’ = {x : x ∈ U and x ∉ A}
Venn diagram representation: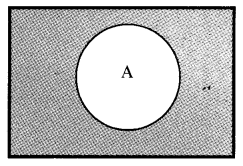

Properties:

1. A’ ∪ A = U, Commutative.
2. A’ ∩ A = φ, Associative
3. (A ∩ B)’ = A’ ∪ B’
4. (A ∪ B)’ = A’ ∩ B’
5. U’ = φ
6. φ’ = U
7. (A)’ = A
8. A – B = A ∩ B’
9. n(A – B) = n(A ∩ B’)
10. n(A) = n(A ∩ B’) + n(A ∩ B)
11. n(A ∪ B) = n(A ∩ B’) + n(A’ ∩ B) + n(A ∩ B)

We hope the Plus One Maths Notes Chapter 1 Sets help you. If you have any query regarding Kerala Plus One Maths Notes Chapter 1 Sets, drop a comment below and we will get back to you at the earliest.