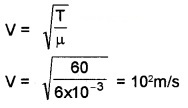Summary
The wave is the propagation of disturbance that carries energy from one point to another point, without translatory motion of particles in the medium. There are three types of wave.
1. Mechanical Wave: Requires medium for propagation.
Eg: Sound wave, Matter wave, Seismic wave, etc.
2. Electromagnetic Wave: No medium for propagation.
Eg: Light, X-rays, UV ray, etc.
3. Matter Wave: Wave associated with moving particles (microscopic particles).
Eg: Wave of moving electron, proton, etc.
Generation of longitudinal waves by tuning for k
When prongs of tuning fork moves outward, it compresses the surrounding air and a region of increased pressure is formed. This region is called condensation. When the prongs move inward a region of low pressure called rarefraction is formed. Thus condensations and rarefractions are alternately produced.
Expression for progressive wave (Displacement relation)
A plane progressive wave propagating along positive direction of ‘x’ is given by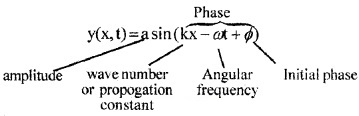
The wave propagating along negative ‘x’ direction is given by y (x, t) = a sin (kx + ωt + Φ).
y(x, t) gives the transverse displacement of element at position x at time t.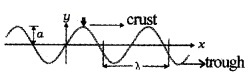
Crust and Trough:
Crust is the point of maximum positive displacement of wave. Trough is the point of maximum negative displacement of wave.
Transverse and Longitudinal Wave
Based on the direction of propogation and vibration wave can be of two types.
| Transverse wave | Longitudinal wave |
| 1. The direction of vibrations of particles of medium is perpendicular to direction of propogation of wave. 2. They travel in the form of crust and troughs 3. Can be polarised Eg: Vibrations in stretched string, light etc. | 1. The direction of vibration of particles of medium is in the direction of propogation of wave. 2. They travel in the form of condensations and rare fractions. 3. Cannot be polarised Vibrations of tuning fork, sound wave, etc. |
Parameters of wave
Amplitude:
The magnitude of maximum displacement of element of the wave from initial position is called amplitude (a).
Phase and initial phase:
The value (kx + ωt + Φ) is called phase and f is the initial phase. The phase gives the state of motion of wave at position ‘x’ and at time V. Initial phase gives initial state of wave.
Wave length (λ):
The linear distance travelled by the wave in one complete oscillation(or vibration). Or it can be defined as distance between two conT secutive crusts or troughs. It is the distance travelled during time period T.
Wave number/Angular wave number/propagation constant:
Wave number ‘k’ is defined as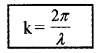
Its unit is radian/m
Time period (T):
Time for one complete oscillation/vibration is called time period.
Frequency (ν):
The number of oscillations/vibrations in one second is called frequency. Its unit is S-1 or Hz (Hetz).
ν =
Angular velocity or angular frequency (ω):
Angular displacement per unit time is called angular velocity or angular frequency.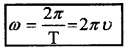
The speed of travelling wave [Relation connecting V, ν and λ]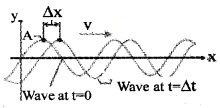
The wave propagating along x direction is represented by y = A sin (kx – ωt + Φ). As wave moves, each point on the wave from (like A) retains its displacement. This is possible only if (kx – ωt) is constant. As the wave moves both x and t are changing to keep (kx – ωt) as constant (x increase with t).
The velocity depends on wavelength and frequency. The wavelength and frequency of wave depends on the properties of medium, i.e. velocity of wave in a medium is determined by
- linear mass density
- Elastic properties.
Speed of wave in stretched string (Transverse wave)
The velocity of wave in stretched string depends on
- linear mass density (µ)
- The tension (T)
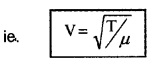
Speed of sound wave (Longitudinal wave)
The speed of sound in medium depends on
- density of medium (ρ)
- Modulus of elasticity
Case: 1( In solid )
If solid has Young’s modulus ‘Y’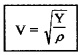
Case: 2( In liquid )
If liquid has Bulk modulus ‘B’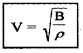
Case: 3 In gas
The speed of sound waves in gas was determined by Newton. According to Newton, condensations and rare fractions are isothermal processes. Hence modulus of elasticity is equal to pressure.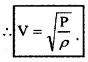
This is called Newton’s formula.
Correction in Newton’s formula.
Question 1.
Find velocity of sound in air using Newton’s formula (P = 1.013 × 105 ρ =1.239 kg m-3)
Answer: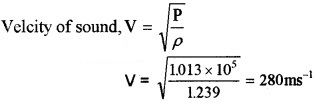
Note: The velocity of sound at STP is found to be 332 ms-1
Laplace’s Formula:
Laplace corrected Newton’s formula taking condensation and rare fraction as adiabatic process. The
modulus of elasticity is now ‘γP‘ where γ = 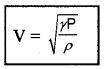
The principle of superposition of waves
It states that when two or more waves pass through a media the net displacement of particle at any time is the algebraic sum of displacements due to each wave.
(or)
The overlapping waves algebraically add to produce a resultant wave.
Reflection of waves
Reflection from rigid boundary:
When a travelling wave is reflected by a rigid boundary, phase reversal (phase difference of π or 180°) will take place.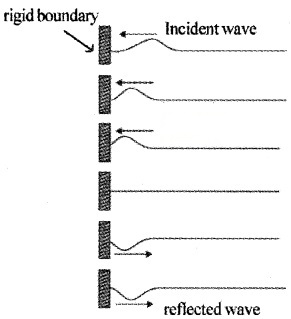
Reflection from open boundary:
When a travelling wave is reflected by an open boundary, no phase change will happen. The incident and reflected wave superimpose to give maximum displacement at boundary.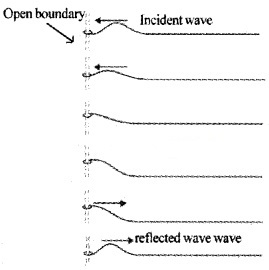
Standing waves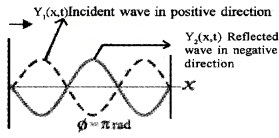
When two waves of same amplitude and frequency travelling in opposite direction superimpose the resulting wave pattern does not move to either sides. This pattern is called standing wave.
The wave travelling in positive direction of x axis y1(x, t) = a sin(kx – ωt)
The wave travelling in negative direction of x axis y2(x, t) = a sin(kx + ωt)
According to superposition Principle, the combined wave is
y(x, t) = y1(x, t) + y2(x, t)
y(x, t) = a sin(kx – ωt) + a sin(kx + ωt)
But sin A + sin B = 2 sin
Hence we get,combined wave as![]()
This wave has an amplitude of ‘2asinkx’, and it is not a moving wave.
Nodes & Antinodes:
The position of maximum amplitude in a standing wave is termed as anti node and position of minimum amplitude (zero) is termed as node.
Node: The amplitude of standing wave is ‘2 a sin kx’. It is zero when kx = 0, π, 2π…. etc.
ie kx = nπ.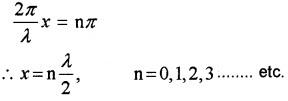
Antinode:
The amplitude has maximum value 2a when (2a sin kx = 2a)
sinkx = 1;
ie; kx = π/2, 3π/2, 5π/2 …… etc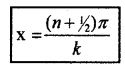
But k =
Hence we get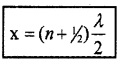
n = 0, 1, 2, 3 etc.
1. Standing Waves In Stretched String & Modes Of Vibration Of String:
A string of length L is fixed at two ends. The position of one end is chosen as x = 0, then the position of other end will be x = L. At x = 0, there will be node. To occur node at x = L, it must satisfy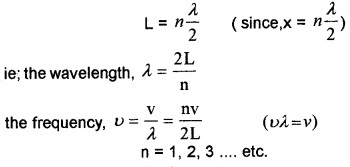
The frequency of vibrations of stretched string of length L is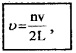
n = 1,2, 3…etc.
This set of frequencies at which the string can vibrate are called natural frequencies or modes of vibration or harmonics. The above equation shows that the modes of vibration (natural frequencies) of string are integral multiple of lowest frequency
n =
Fundamental mode(or) First harmonics:
For n = 1
ν1 =
This is the lowest frequency with which string vibrates. This is called fundamental mode or first harmonic of vibration.
Relation between I and L for first harmonics:
The string vibrate in a single segment as shown in figure.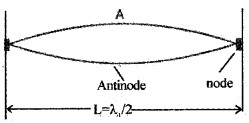
Second harmonic: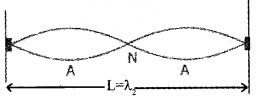
For n = 2
Relation between I and L for second harmonics![]()
Third harmonic: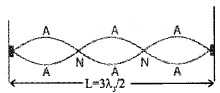
For n = 3, there is 3rd harmonic. Thus collection of all possible mode is called harmonic series and n is called harmonic number.
2. Vibrational modes of an air column:
(a) In closed tube:
In closed tube one end is closed and other end is open. Air column in a glass tube partially filled with water is an example of closed system. The air column in tube can be set into vibrations with the help of air excited by tuning fork.
The longitudinal waves thus generated is reflected at the closed end and a node is formed there [reflected and incident wave are out of phase and at the closed end, they superimpose to give minimum displacement]. At the open end, the displacement is maximum and antinode is formed. If L is the length of air column, anti node occurs at x = L.
We know the condition for antinode x = (n + 1/2) λ/2
Therefore L = (n + 1/2) λ/2
for n = 0, 1, 2, …….etc.
The wavelength, λ =
for n = 0, 1, 2, …. etc.
The frequency ν = (n + 1/2)
for n = 0, 1, 2, …….etc.
From this equation, it is clear that the air column can vibrate with different modes of frequencies (normal modes or harmonics)
Fundamental Mode(or) First harmonic:
We get fundamental mode when n=0 Substitute this in eq(2), we get
ν1 =
This is the fundamental frequency. The higher frequencies are odd harmonics of fundamental frequency ie;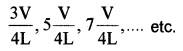
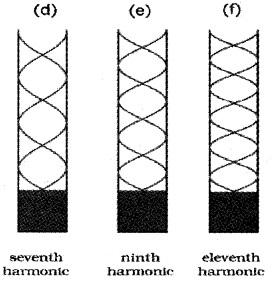
(b) Open tube:
In open tube, both ends are open. At both ends, antinodes are formed.
The condition to get antinode x = n λ/2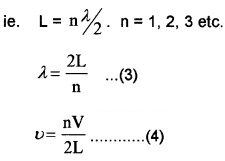
The frequency (fundamental frequency):
We will get fundamental frequency in open tube,when n = 1. Substitute this in eq(4)
ν1 =
In open pipe all harmonies are generated whereas in closed pipe only odd harmonies are generated.
For n = 2, ν2 = 2
For n = 3, ν3 = 3
ν2 = 2 ν1 & ν3 = 3 .ν1. Thus both odd and even harmonics are generated.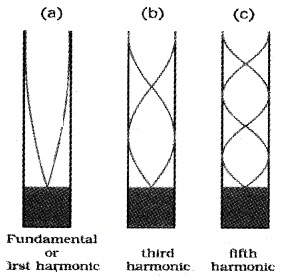
Beats:
When two sound waves of nearly same frequency and amplitude travelling in same direction super imposed and periodic variation of sound intensity (wavering of sound or waxing and waning of sound) is produced. This is called beats.
Explanation:
If two tuning forks of slightly different frequencies are sounded together, a regular rise and fall of sound can be heard. The sound travels in the form of condensation and rarefactions.
When two condensations due to two notes reach our ear at the same time, they superimpose to get maximum intensity (waxing of sound). If two rarefactions are reached simultaneously, they superimpose to get minimum intensity (waning of sound).
Analytical treatment of beats
Beats frequency
Suppose two sound waves of u1 and u2 propagating in the same direction through a medium. For simplicity let the listener be situated at x = 0 and the amplitudes of waves to be equal ie. a1 = a2 = a.
The displacements y1 and y2 due to each wave are given by
y1 = a sin2pu1t and y1 = a sin2pu2t
According to super position principle, the resultant displacement at the same time t is
y = y1 + y2
= a sin2pu1t + a sin2pu2t
y = a [sin2pu1t + sin2pu2t]
It is clear that, the amplitude of resultant wave (A) changes with time. It shows maxim and minima.
The resultant amplitude will be maximum, if,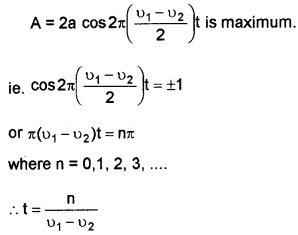
Hence the amplitude of the resultant wave will be maximum at times![]()
Time interval between successive maxima =
resultant amplitude will be minimum if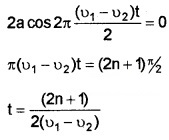
Time internval between two consecutive minima =
Frequency of minima = ν1 – ν2
Graphical representation of beats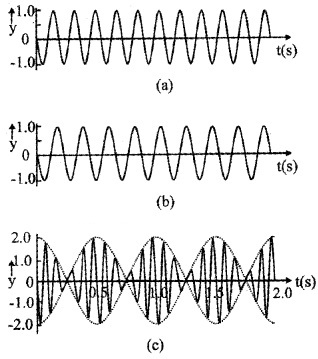
Doppler Effect
The apparent change in the frequency of sound wave due to the relative motion of source or listener or both is called Doppler effect. It was proposed by John Christian Doppler and it was experimentally tested by Buys Ballot.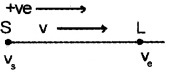
Considers source is producing sound of frequency n. Let V be the velocity of sound in the medium and I the wavelength of sound when the source and the listener are at rest. The frequency of sound heard by the listener is
ν =
Let the source and listener be moving with velocities vs and vl in the direction of propogation of sound from source to listener. (The direction S to L is taken as positive)
The relative velocity of sound wave with respect to the source = V – Vs.
Apparent wavelength of sound,
λ1 =
Since the listener is moving with velocity v f, the rela¬tive velocity of sound with respect to the listener,
V1 = V – Vl _____(2)
Question 2.
A string fixed one end is suddenly brought in to up and down motion.
- What is the nature of the wane produced in the string and name the wave?
- A brass wire 1 m long has a mass 6 × 10-3 kg. If it is kept at a tension 60N, What is the speed of the wave on the wire?
Answer:
1. Transverse wave
2.