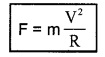Kerala Plus One Physics Notes Chapter 4 Motion in a Plane

 Summary

Introduction
In this chapter, we will study, about vector, its ’ addition, substraction and multiplication We then discuss motion of an object in a plane. We shall also discuss uniform circular motion in detail.

Scalars And Vectors

a. Scalars:
A quantity which has only magnitude and no direction is called a scalar quantity.
Eg: length; volume, mass, time, work etc.

b. Vectors:
(i) The need for vectors:
In one dimensional motion, there are only two possible directions. But in two or three dimensional motion, infinite number of directions are possible. Hence quantities like displacement, velocity, force etc. cannot be represented by magnitude alone: Therefore in order to describe such quantities, not only magnitude but direction also is essential.

(ii) Vector:
A physical quantity which has both magnitude and direction is called a vector quantity.
Eg: Displacement, Velocity, Acceleration, Force, momentum.

1. Position and Displacement Vectors:
Position vector:
Consider the motion of an object in a plane. Let P be the position of object at time tw.r.t.origin given O.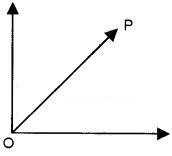

A vector representing the position of an object P with respect to an origin O is called position vector OP−→− of the object. This position vector may be represented
by an arrow with tail at O and head at P.

The length of the line gives the magnitude of the vector and arrow head (tip) indicates its direction in space. The magnitude of OP is represented by |OP−→−|.

Displacement vector: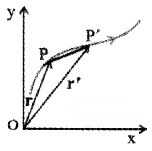

Consider the motion of an object in a plane. Let P be the position of a moving object at a time t and p1 that at a later time t1. OP−→− and OP1−→− are the position vectors at time t and t1 respectively. So the vector PP1−→− is called displacement vector corresponding to the motion in the time interval (t – t1).

2. Equality of vectors:
Two vectors are said to be equal if they have the same magnitude and direction.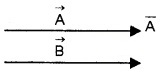

The above figure shows two vectors A⃗  and B⃗  having the same magnitude and direction.
∴ A⃗  = B⃗ .

Question 1.
Observe the following figures (a) and (b) and find which pair does represents equal vectors?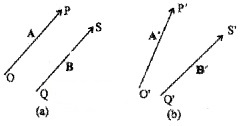

Answer:
Figure a represent that A and B are equal vectors. Two vectors A1 and B1 are unequal, because they were in different directions.

Multiplication Of Vectors By Real Numbers
Multiplying a vector 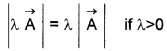A⃗  with a positive number I gives a vector whose magnitude is changed by the factor λ.

The direction λA⃗  is the same as that of A⃗ .
Examples: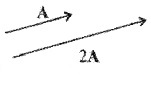

A vector 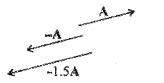A⃗  and the resultant vector after multiplying A⃗  by a positive number 2.

A vector A and resultant vector after multiplying it by a negative number-1 and -1.5.

Addition And Subtraction Of Vectors – Graphical Method
Vectors representing physical quantities of the same dimensions can be added or subtracted. The sum of two or more vectors is known as their resultant.

1. When two vectors are acting in the same direction:

2. When two vectors act in opposite direction:
In this case, the angle between the vectors is 180°.

The resultant of the two vectors is a new vector whose magnitude is the difference between the magnitudes of the two vectors and whose direction is the same as the direction of the bigger vector.

3. When two vectors are inclined to each other:
The sum of two vectors inclined at an angle q can be obtained either by

• the law of triangle of vectors
• the parallelogram law of vectors

(i) Triangle method:
This law states that if two vectors can be represented in magnitude and direction by the two sides of a triangle taken in the same order, then the resultant is represented in magnitude and direction by the third side of the triangle taken in the reverse order.

Explanation
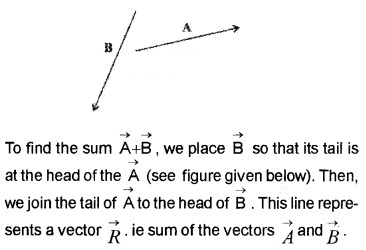
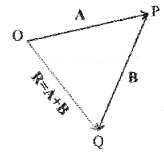
Consider two vectors A⃗  and B⃗  as shown in figure.

(ii) Parallelogram law of vector addition:
This law states that if two vectors acting at a point can be represented in magnitude and direction by the two adjacent sides of a parallelogram, then the diagonal of the parallelogram through that point represents the resultant vector.
Explanation
Consider two vectors A⃗  and B⃗  as shown in figure.

To find A⃗  + B⃗ , we bring theirtails to a common origin Q as shown below.


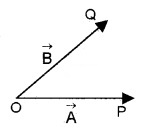
The diagonal of parallelogram OQSP, gives the resultantof (R⃗  = A⃗  + B⃗ ) of two vectors A⃗  and B⃗ .
Note: Triangle and parallelogram law of vector addition gives the same result, ie. the two methods are equivalent.

4. Substraction of vectors: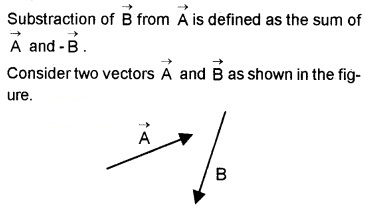

To substract 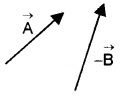B⃗  from A⃗ , reverse the direction of B⃗ .

Then add –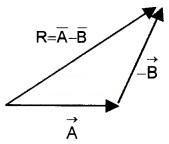B⃗  with A⃗  using parallelogram law or tri¬angle law.

The resultant of A⃗  and B⃗  is given by R⃗ .
Null vector or zero vector:
A vector having zero magnitude is called a zero vector or null vector. Null vector is represented by O⃗ . Since the magnitude is zero, we don’t have to specify its direction.
Properties of null vector:

Question 2.
Explain a zero vector using an example.
Answer:
Suppose that an object which is at P at time t, moves to p1 and then comes back to P. In this case displacement is a null vector.

Resolution Of Vectors Unit Vectors
A vector divided by its magnitude is called a unit vector along the direction of that vector. A unit vector in the direction of 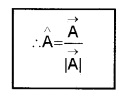A⃗  is written as A^.

Orthogonal unit vectors: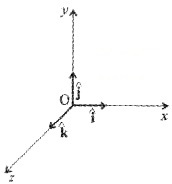

In the Cartesian coordinate system, the unit vectors along the X, Y and Z directions are represented by i^, j^ and k^ respectively and are known as orthogonal unit vectors.
For unit vectors

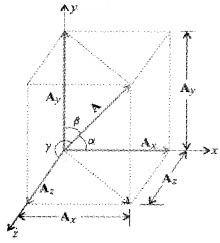
Resolution of vector into rectangular components:
The components of a vector in two mutually perpendicular directions are called its rectangular components.
Explanation

Consider a vector 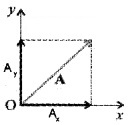A→ that lies in x-y plane as shown in figure. To resolve A→, draw lines from the head of A→ perpendicularto the coordinate axes as shown below.

The quantities Ax and Ay are called x and y components of the vector A→. Hence the vector A→ can be written in terms of rectangular components as

Magnitude of A→:

From the figure, the magnitude of 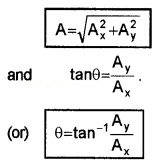A→ can be written as,

Question 3.
A vector A→ in xyz plane is given below. Ax, Ay and Az are the perpendicular components in x,y and z directions respectively.

1. Write A→ in terms of rectangular components.
2. Write the magnitude of A→.

Answer:

The magnitude of vector 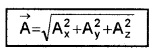A→ is

Vector Addition – Analytical Method
The graphical method of adding vectors helps us in visualizing the vectors and the resultant vector. But this method has limited accuracy and sometimes tedious. Hence we use the analytical method to add vectors.
Explanation

The vectors obey commutative and associative laws. Hence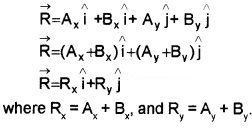

Question 4.
Find the magnitude and direction of the resultant of two vectors A→ and A→ in terms of their magnitudes and angle between them.
Answer: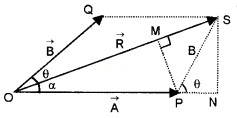

Consider two vectors A⃗ (=OP−→−) and B⃗ (=OQ−→−) making an angle q. Using the parallelogram method of
vectors, the resultant vector R→ can be written as,

SN is normal to OP and PM is normal to OS. From the geometry of the figure
OS2 = ON2 + SN2
but ON = OP + PN
ie. OS2 = (OP+PN)2 + SN2 ______(1)
From the triangle SPN, we get
PN = Bcosq and SN = Bsinq
Substituting these values in eq.(1), we get
OS2 = (OP + Bcosq)2 + (Bsinq)2
But OS = R and OP = A
R2 = (A + Bcosq)2 + B2sin2q
= A2 + 2ABcosq + B2cos2q + B2sin2q
R2 = A2 + 2 ABcosq + B2

The resultant vector 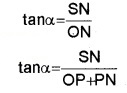R→ make an angle a with \overrightarrow{\mathrm{A}}. From the right angled triangle OSN,

But SN = Bsinq PN = Bcosq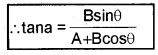

Motion In A Plane

1. Position vector and displacement vector Position vector: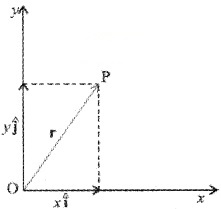

Consider a small body located at P with reference to the origin O. The position vector of the point ‘P’

Displacement vector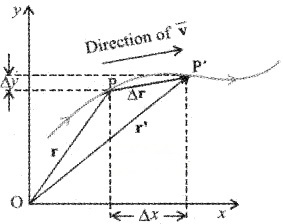

where Dx = x1 – x1, Dy = y1 – y
Velocity:
If Dt is the time taken to reach from P to P1
The average velocity, v→av=Δr−→Δt ____(3)
Substitute eq.(2) in eq.(3), we get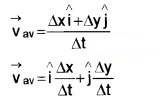

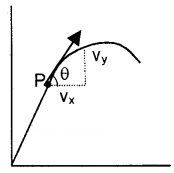
The direction of average velocity is the same as that of Δr−→.
The instantaneous velocity can be written as

Acceleration:
If the velocity of an object changes from 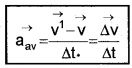v→ to v1→ in time Dt, then its average acceleration is given by

Instantaneous acceleration:
The acceleration at any instant is called instantaneous acceleration. When Dt goes to zero, the average acceleration becomes instantaneous acceleration.
ie. Instantaneous acceleration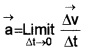

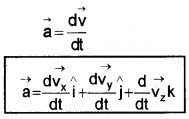
Motion In A Plane With Constant Acceleration
Consider an object moving in XY plane with a constant acceleration ‘a’. Let u⃗  be the initial velocity at t=0 and v⃗  be the final velocity at time t.
Then by definition acceleration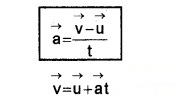

In terms of components
vx = ux + axt
vy = uy + ayt
Displacement in a plane
If r0→ and r⃗  be position vectors of particle at t = 0 and time t respectively, then
displacement = r⃗ −r⃗ 0 _______(1)
For uniformly accelerated motion, displacement,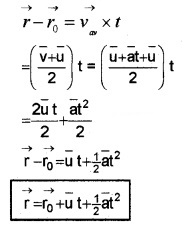

In terms of components
x = x0 + uxt + 1/2 axt2
y = y0 + uyt + 1/2 ayt2
The eq.(2) shows that, the above motion in xy plane can be treated as two separate one-dimensional motions along two perpendicular directions.

Relative Velocity In Two Dimensions
Consider two bodies A and B moving along a plane with velocities V→A and V→B. Then the velocity of A relative to that of B is,

Similarly velocity of B relative to that of A

Projectile Motion
Projectile:
A body is projected into air and is allowed to move under the influence of gravity is called a projectile.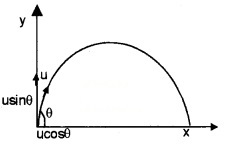

Consider a body which is projected into air with a velocity u at an angle q. The initial velocity ‘u’ can be divided into two components ucosq along horizontal direction and using along vertical direction.

1. Time of flight:
The time taken by the projectile to cover the horizontal range is called the time of flight. Time of flight of projectile is decided by usinq. The time of flight can be found using the formula
s = ut + 1/2 at2
Taking vertical displacement s = 0, a = -g and initial vertical velocity = u sin q, we get
0 = usinqt – 1/2gt2
1/2 gt2 = usinqt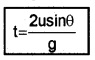

2. Vertical height:
Vertical height of body is decided by vertical component of velocity (usinq). The vertical displacement of projectile can be found using the formula v2 = u2 + 2as
When we substitute v=0, a = -g, s = H and u = usinq, we get
0 = (usinq)2 + 2 – g × H
2gH = u2sin2q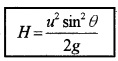

3. Horizontal Range:
If we neglect the air resistance, the horizontal velocity (ucosq) of projectile will be constant.
Hence the horizontal distance (R) can be found as
R = horizontal velocity × time of flight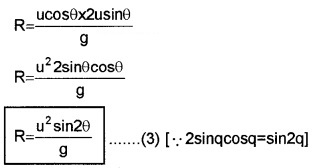

The eq.(3) shows that, R is maximum when sin2q is maximum, ie. When q0 = 45°.
The maximum horizontal range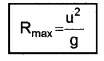

Equation for path of projectile

Question 5.
What is the shape of path followed by the projectile? Show that the path of projectile is parabola. The vertical displacement of projectile at any time t, can be found using the formula.
Answer:
S = ut+ 1/2at2
y = usinqt – 1/2gt2
But we know horizontal displacement, x = ucosq × t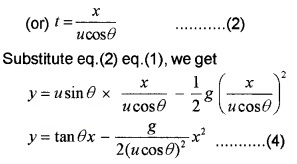

In this equation g, q and u are constants. Hence eq.(4) can be written in the form
y = ax + bx2
where a and b are constants. This is the equation of the parabola, ie. the path of the projectile is a parabola.

Uniform Circular Motion
The motion of an object along the circumference of a circle is called circular motion.
Uniform circular motion:
When an object follows a circular path at a constant speed, the motion is called uniform circular motion.
Period:
The time taken by the object to complete one full revolution is called the period.
Frequency:
The number of revolutions completed per second is called the frequency u of the circular motion.
If the period of a circular motion isT, its frequency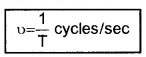

Angular Displacement (Dq):
The angle Dq in radians swept out by the radius vector in a given interval of time is called the angular displacement of the object.
Angular velocity:
The rate of change of angular displacement is called the angular velocity.

If T is the period of an object, then its radius vector sweeps out an angle of 2p radian.
Therefore in one second it sweeps out an angle 2πT.
∴ Angular velocity of the object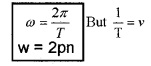

Expression for velocity and acceleration in uniform circular motion: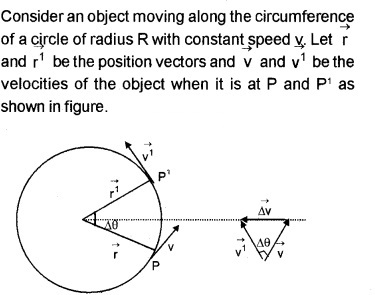

The direction of velocity is in the direction of tangent at that point. The change in velocity vectors (Δv−→) is obtained by triangle law of vector as shown in figure (b).

a. Speed and angular speed in uniform circular motion:
Let the Dq be the angle constructed by the body during the time interval ∆t. The angular velocity can be written as

If the distance travelled by the object during the time Dt is Dr (ie. PP1 = Ds) then speed

But Ds = RDq
where R = |r⃗ |=|r′→|
Substituting Dr = RDq in eq.(1)
we get

b. Acceleration in uniform circular motion:

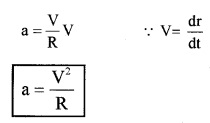
The direction of this acceleration should be in the direction of 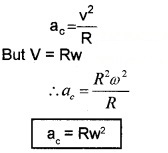ΔV−→−. Fig (b) shows that ΔV−→− is towards the centre of the circular path. Hence the acceleration is directed towards the centre of the circle and is called centripetal acceleration.

The force which produces this centripetal acceleration is called centripetal force.
Centripetal force can be written as
F = mac

But ω = VR. Hence we get K