Kerala Plus One Maths Notes Chapter 3 Trigonometric Functions

 

I. Angles
The measure of an angle is the amount of rotation performed to get the terminal side from the initial side.

1. Degree measure: If a rotation from the initial side to terminal side is (1360)th of a revolution, the angle is said to have a measure of one degree, written as 1°. 1° = 60′ and f = 60″.

2. Radian measure: An angle subtended at the center by an arc of length 1 unit in a unit circle is said to be of 1 radian. Radian measure is a real number corresponding to degree measure.

180° = π radians

Radian measure = π180 × Degree measure

Degree measure = 180π × Radian measure

l = rθ, where l = arc length, r = radius of the circle and θ = angle in radian measure.

II. Trigonometric Function
Consider a unit circle with centre at the origin of the coordinate axis.
Let P (a, b) be any point on the circle which makes an angle θ° with the x-axis. Let x be the corresponding radian measure of the angle θ°, i.e; x is the arc length corresponding to θ°.

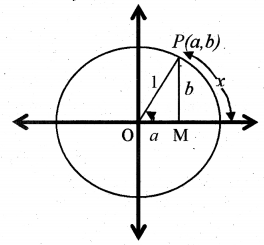
From the ∆OMP’m the figure we get;
sin θ = sin x = b1 = b and cos θ = cos x = b1 = a
This means that for each real value of x we get corresponding unique ‘sin’ and ‘cosine’ value which is also real. Hence we can define the six trigonometric functions as follows.

1. f : R → [-1, 1] defined by f(x) = sin x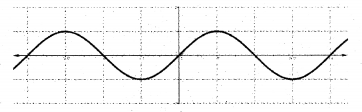

2. f : R → [-1, 1] defined by f(x) = cos x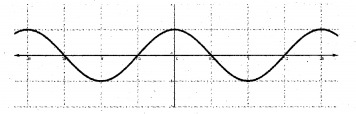

3. f : R – {nπ, n ∈ Z} → R – (-1, 1) defined by f(x) = 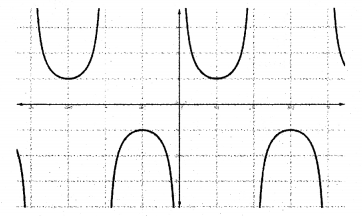1sinx = cosec x

4. f : R – {(2n + 1) 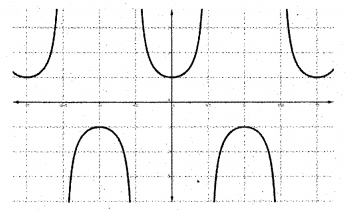π2} → R – (-1, 1) defined by f(x) = 1cosx = sec x

5. f : R – {(2n + 1)π, n ∈ Z} → R defined by f(x) = 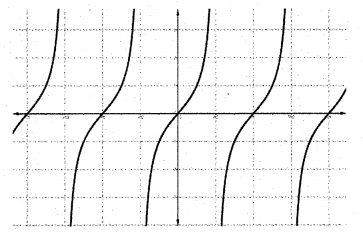sinxcosx = tan x

6. f : R – {nπ, n ∈ Z} → R defined by f(x) = 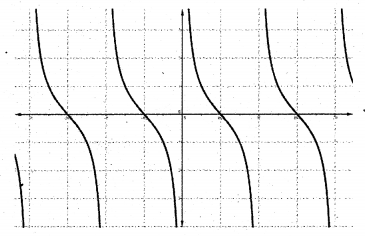cosxsinx = cot x

Sign of trigonometric functions in different quadrants;

For odd multiple of π2 trignometric functions changes as given below.
sin → cos
cos → sin
sec → cosec
cosec → sec
tan → cot
cot → tan

The value of trigonometric functions for some specific angles;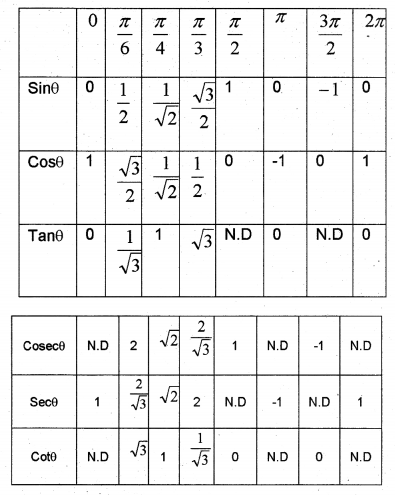

III. Compound Angle Formula

sin(x + y) = sin x cos y + cos x sin y

sin(x – y) = sin x cos y – cos x sin y

cos(x + y) = cos x cos y – sin x sin y

cos(x – y) = cos x cos y + sin x sin y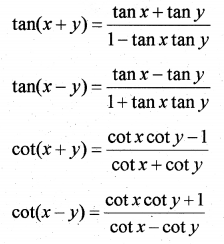

sin(x + y) sin(x – y) = sin² x – sin² y = cos² x – cos² y

cos(x + y) cos(x – y) = cos² x – sin² y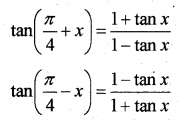

IV. Multiple Angle Formula

cos2x = cos² x – sin² x
= 1 – 2sin² x
= 2 cos² x – 1
= 1−tan2x1+tan2x

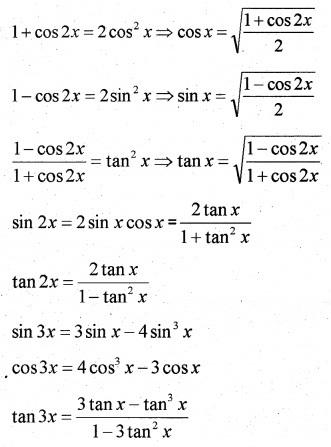
V. Sub-Multiple Angle Formula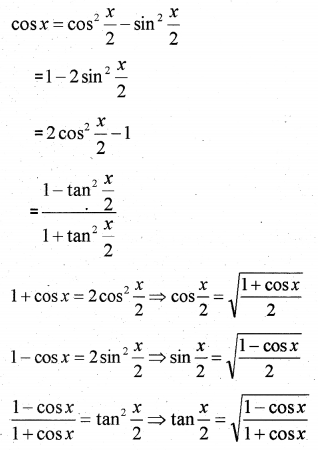

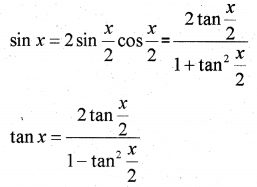
VI. Sum Formula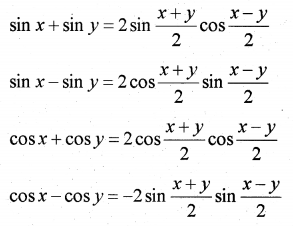

VII. Product Formula

2 sin x cos y = sin(x + y) + sin(x – y)

2 cos x sin y = sin(x + y) – sin(x – y)

2 cos x cos y = cos(x + y) + cos(x – y)

2 sin x sin y = cos(x – y) – cos(x + y)

VIII. Solution of Trigonometric Equations

sin x = 0 gives x = nπ, where n ∈ Z

cos x = 0 gives x = (2n + 1)π, where n ∈ Z

tanx = 0 gives x = nπ, where n ∈ Z

sin x = sin y ⇒ x = nπ + (-1)ⁿ y, where n ∈ Z

cos x = cos y ⇒ x = 2nπ ± y, where n ∈ Z

tan x = tan y ⇒ x = nπ + y, where n ∈ Z

Principal solution is the solution which lies in the interval 0 ≤ x ≤ 2π.

IX. Sine and Cosine formulae

Let ABC be a triangle. By angle A we mean the angle between the sides AB and AC which lies between 0° and 180°. The angles B and C are similarly defined. The sides AB, BC, and CA opposite to the vertices C, A, and B will be denoted by c, a, and b, respectively.

Theorem 1 (sine formula): In any triangle, sides are proportional to the sines of the opposite angles. That is, in a triangle ABC
sinAa=sinBb=sinCc

Theorem 2 (Cosine formulae): Let A, B and C be angles of a triangle and a, b and c be lengths of sides opposite to angles A, B, and C, respectively, then
a² = b² + c² – 2bc cos A
b² = c² + a² – 2ca cos B
c² = a² + b² – 2ab cos C

A convenient form of the cosine formulae, when angles are to be found are as follows: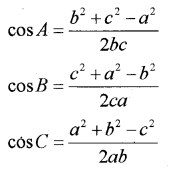

We hope the Plus One Maths Notes Chapter 3 Trigonometric Functions help you. If you have any query regarding Kerala Plus One Maths Notes Chapter 3 Trigonometric Functions, drop a comment below and we will get back to you at the earliest.